GCD+LCM
Display


(HP-41CX, Hewlett Packard 1983 and DM41X, SwissMicros 2020)
Overview
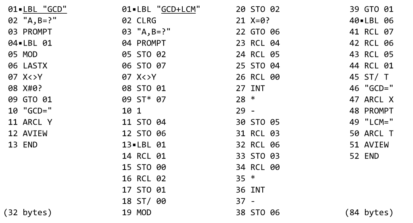
Programs GCD calculates the Greatest Common Divider of two integer values. GCD uses a very simple and short algorithm. Its big friend GCD+LCM calculates both the Greatest Common Divider and the Least Common Multiple according to the Knuth algorithm (see also the similar program for the HP-67 at the MoHPc).
Algorithm
Given two integer values A and B of which the GCD and LCM can be determined as follows:
yi+1 = si xi+1 = ti
si+1 = (ai div bi).si + yi ti+1 = (ai div bi).ti + xi
ai+1 = bi bi+1 = ai mod bi
where: s0 = 0, y0 = 1 t0 = 1, x0 = 0
and: a0 = A b0 = B
The GCD follows from ai+1 if the value bi+1 equals 0 (zero): ai+1 = GCD(A,B)
The LCM follows from: LCM(A,B) = A.B / GCD(A,B)
Example (1)
Please note my default FIX 5 setting in de examples below for the codes.

Example (2)
Below example decrypts a numerical sequence back to a text.

Program Listing
The listing of both the GCD and GCD+LCM programs is given below:
Downloads
PDF format of programs GCD and GCD+LCM.
RAW/TXT format of programs GCD and GCD+LCM (in zip file).
© 1999-2020 by Auke Hoekstra





























 2017
2017 2020
2020 2020
2020 2013
2013 2011
2011 2014
2014 2016
2016 2018
2018 2010
2010 2022
2022 2019
2019 2013
2013 2014
2014 2019
2019 2018
2018 2023
2023 2016
2016 2015
2015 2019
2019 2023
2023 2013
2013 2023
2023