ROMAN
Display
(HP-41CX, Hewlett Packard 1983 and DM41X, SwissMicros 2020)
Overview
Programs R2N (and R3N) and N2R convert decimal (Arabic) numbers to Roman notation and vice versa. The number conversion goes from 1-3999.
Many conversion programs have been created by several users aiming to build with the least number of bytes for the programs. The programs in this document require HP-41CX functions XTOA and ATOX. The main difficulty with the conversion to and from Roman numbers is the so-called subtractive rule. To convert numbers correctly the conversion rules are to be followed precisely. Here is a short summary. Roman numerals are written using seven different letters: I, V, X, L, C, D and M, they represent the numbers 1, 5, 10, 50, 100, 500 and 1,000. The use these seven letters makes up thousands of others. For example, the Roman numeral for 2 is written as ‘II’ which is just two 1’s smushed together. The number 12 is XII which is just X (10) + II (2). Taking it a step further, the number 27 is written as XXVII, which when broken down looks like XX (20) + V (5) + II (2); all totaled up it equals to 27.
Roman numerals are usually written largest to smallest from left to right. However, this is not always true. The Romans didn’t like writing four of the same numerals in a row, so they developed a system of subtraction.
The Roman numeral for 3 is written III, but 4 is not IIII. Instead, the subtractive principle is used. The number 4 is written as ‘IV’. It shows the I (1) before V (5) and because the smaller number is before the larger number, it must be subtracted here – giving the value 4 for IV. The same principle applies to the number 9, which is written as IX.
There are six instances where subtraction is used:
- I can be placed before V (5) and X (10) to make 4 and 9.
- X can be placed before L (50) and C (100) to make 40 and 90.
- C can be placed before D (500) and M (1000) to make 400 and 900.
The number 994 is a great example of this rule – it’s written CMXCIV. Broken down we have CM = 900, XC = 90 and IV = 4; adding all these up results in 994.
The solution approach to code the algorithm is from Sriharsha Sammeta as described in: https://www.geeksforgeeks.org/converting-decimal-number-lying-between-1-to-3999-to-roman-numerals/amp/.
Conversion
The solution approach follows the algorithm in which the normal and subtractive rules are implemented in a straightforward manner. In this approach the MainSignificantDigit in the number is considered first. For example, in 1234, the main significant digit is 1. Similarly in 345 it is 3.
To extract the main significant digit out, a divisor (div) like 1000 for 1234 (since 1234 / 1000 = 1) is required which is 100 in the case of 345 is 3 (345 / 100).
A lookup called RomanNumeral is defined as =
{1 : ‘I’, 5: ‘V’, 10: ‘X’, 50: ‘L’, 100: ‘C’, 500: ‘D’, 1000: ‘M’}
For each digit in the decimal number, the following logic applies (in which div refers to the Roman base):
if MainSignificantDigit <= 3
RomanNumeral [div] * MainSignificantDigit
if MainSignificantDigit == 4
RomanNumeral [div] + RomanNumeral [div*5]
if 5 <= MainSignificantDigit <= 8
RomanNumeral [div*5] + (RomanNumeral [div] * (MainSignificantDigit-5))
if MainSignificantDigit == 9
RomanNumeral [div] + RomanNumeral [div*10]
Here is an example: suppose the input number is 3984:
Iteration 1: Initial number = 3984
MainSignificantDigit is 3; div = 1000. RomanNumeral [1000] * 3 gives: MMM
Iteration 2: Updated number = 984
MainSignificantDigit is 9; div = 100.
RomanNumeral [100] + RomanNumeral [100*10] gives: CM
Iteration 3: Updated number = 84
MainSignificantDigit is 8; div = 10.
RomanNumeral [10*5] + RomanNumeral [10]*(8-5) gives: LXXX
Iteration 4: Updated number = 4
MainSignificantDigit is 4; div = 1.
RomanNumeral [1] + RomanNumeral [10*5] gives: IV.
The result by clubbing all the above gives MMMCMLXXXIV for the number 3984.
Examples (1): N2R
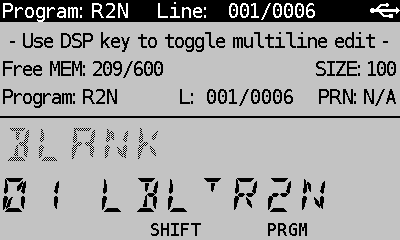
Examples (2): R2N
Please note that my default FIX 5 setting which can be replaced by your preferred number of decimals.
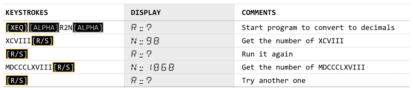
Program Listing
The listing of programs N2R (Numerical to Roman) is given below:
and for R2N (Roman to Numerical) shown here:
The alternative of R2N is listed as R3N (with hard coded initialisation):
Registers, Labels and Flags
Downloads
PDF format of programs N2R, R2N and R3N.
RAW/TXT format of programs N2R, R2N and R3N (in zip file).
© 1999-2023 by Auke Hoekstra
