CRT
Display
(HP-41CX, Hewlett Packard 1983 and DM41X, SwissMicros 2020)
Overview
The CRT program represents a solution to the Chinese Remainder Theorem which states that a linear system of congruence equations with pairwise relatively prime moduli has a unique solution modulo the product of the moduli of the system.
Practically, it goes like this. Imagine a basket of eggs for which it is not known how many there are. Too lazy to count all of them one may know that if you take out three at a time, it ends up with two left-over. If one takes out five at a time, three are left-over, and by taking out seven at a time, two are left-over. This is enough information to figure out the least number of eggs that are in the basket. Here we go.
The basis for finding a solution for an integer number X which satisfies the congruences of modulo definitions as explained below.
Suppose that m1, m2,..,mk are pairwise relatively prime positive integers, and a1, a2,..,ak a series of integers, congruences exist as follows:
x ≡ ai (mod mi) for i=1..k and have a unique solution:
M = m1·m2·..·mk which is given by:
x ≡ a1M1y1 + a2M2y2 + .. + akMkyk (mod M) with:
Mi = M/mi and yi ≡ 1/Mi (mod mi) for i=1..k
The values yi can be found by applying the Extended Euclidean Algorithm.
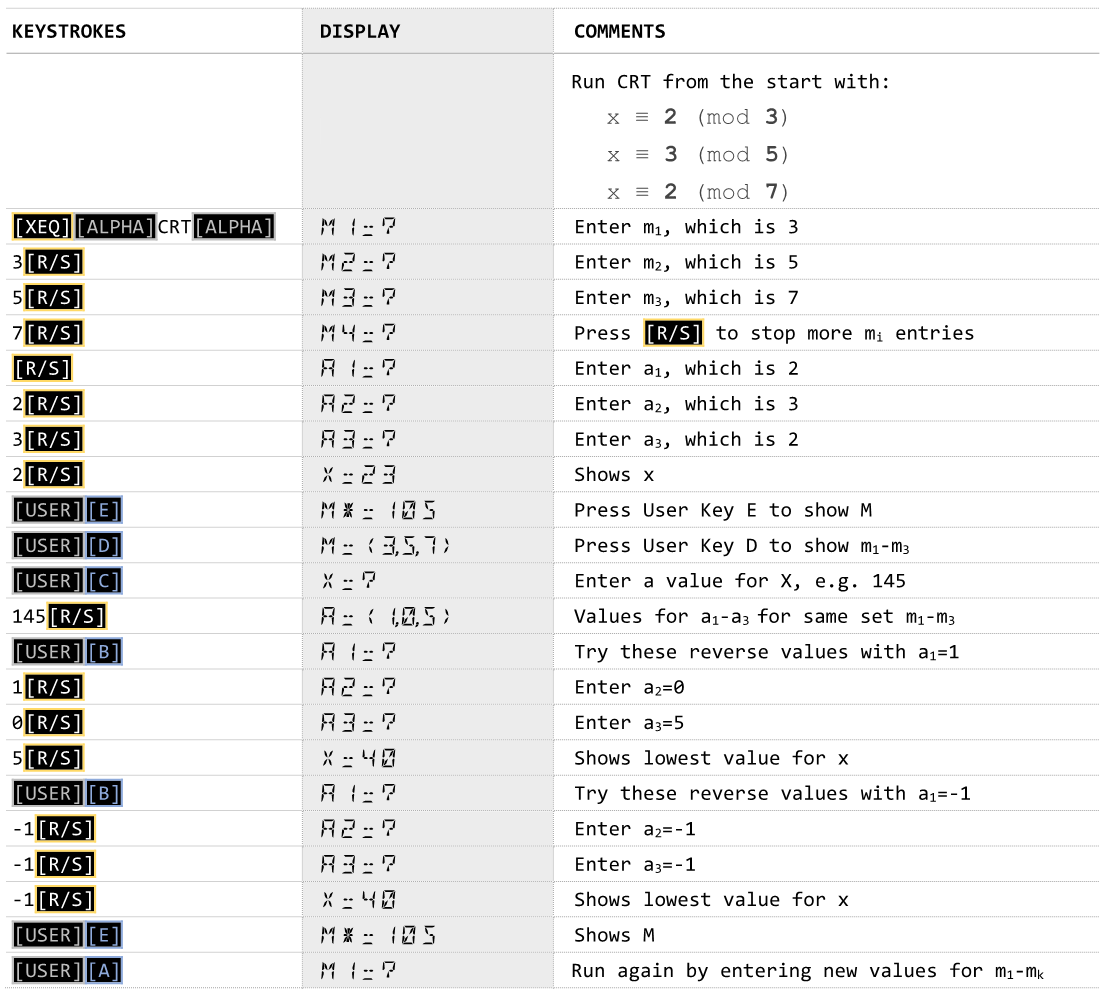
Example 1
Please note that my default FIX 5 setting which can be replaced by your preferred number of decimals at line 178. An example are the following three congruences:
x ≡ 2 (mod 3)
x ≡ 3 (mod 5)
x ≡ 2 (mod 7)
in which M=LCM(3,5,7)=105 and the value of x is to be determined.
Example 2
Please note that my default FIX 5 setting which can be replaced by your preferred number of decimals at line 179. An example are the following three congruences:
x = 5 (mod 7)
x = 7 (mod 11)
x = 14 (mod 31)
x = 8 (mod 45)
in which M=LCM(7,11,31,45)=107415 and the value of x is to be determined.
Program Listing
The listing of CRT is given below with functions A-E in User Mode.
Registers, Labels and Flags
Downloads
PDF format of program CRT.
RAW/TXT format of program CRT (in zip file).
References
Mathematical article: Chinese Remainder Theorem by University of Colorado Denver.
Interactive math website: Chinese Remainder Theorem by Cut the Knot.
© 1999-2020 by Auke Hoekstra
