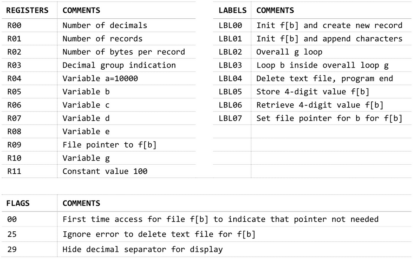
PIDTW
Display
(HP-41CX, Hewlett Packard 1983 and DM41X, SwissMicros 2020)
Overview
The PIDTW can calculate the decimals of PI according to the method by Beeler et al. in 1972. It approximates PI that gives an additional bit of precision with 14 terms giving 4 decimal digits of precision each time because 214 > 104. Therefore 2800 = 14·200 terms are used. The author of a very compact C program, Dik T. Winter (hence DTW in the program name), wrote the following 160 characters’ code:
int a=10000,b,c=2800,d,e,f[2801],g;main(){for(;b-c;)f[b++]=a/5;
for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)for(b=c;d+=f[b]*a,
f[b]=d%--g,d/=g--,--b;d*=b);}
which can be reformatted to something more readable:
int a=10000,b,c=2800,d,e,f[2801],g;
int main() {
b=0;
while(b
f[b]=a/5;
}
d=0;
g=c*2;
while(g>0) {
b=c;
while((b>0)) {
d=d*b+f[b]*a;
g=g-1;
f[b]=d%g;
d=d/g;
g=g-1;
b=b-1;
}
c=c-14;
printf("%.4d", e+d/a);
e=d%a;
g=c*2;
}
return 0;
}
which gives the terms as 4 digits with tens to hundreds of iterations around the variable-g-while-loop and hundreds to thousands of iterations around the variable-b-while-loop. For this program to understand its feasibility, the requirements for the array size and the number of iterations were analysed before writing a program for the HP-41CX. It turns out that for each decimal it requires 3.5 times as many terms as well as array size. For example, for 800 decimals, it requires 2800 terms to be calculated and an array with 2800 values. The number of loops for b increases exponentially which, together with the required memory for the array f[..] brings limitations due to the capability of the calculator. Having mentioned that, it is feasible to determine the decimals up to 120. From the C program, it has been verified that the values in array f[..] are positive integers that remain under 10000. The solution for storing and updating array f[..] is found in using an ASCII file, thereby converting the 4 digits number in one pair of ASCII converted bytes. Each number in f[..] requires therefore 2 bytes. The alternative of storing each number in a register would require too much memory. The design of the program is explained later.
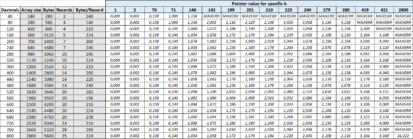
The values of PI are displayed in the table below for reference. This grouping of 4 decimals is how the program will show the results. The rows up to 120 decimals have been marked in both tables.
Design
The key problem with this algorithm is handling the values of the array f[..]. The solution built for this program is to store each value as ASCII bytes in a file. One file record can store up to 254 bytes which implies a maximum 127 values of f[..]. To make the process repeatable, the number of bytes must be even and fit precisely in each defined number of records (without empty space at the end). In the first table the best fit of number of records and number of bytes per record is given. This is the basis for storing all values of f[..]. As this is not linear, the number of records is retrieved from 2 alpha-based lookup vectors in lines 15-20. These have been marked with dotted lines in the table.
The values of f[..] are stored in the ASCII file PIF via routine 05 (line 154) and retrieved via routine 06 (line 178). To make these routines fast a number wxyz is encrypted and decrypted as follows:
- Encryption of f[..] = wxyz starts with splitting it into two numbers wx and yz
- To avoid the NULL character, 100 is added to wx and 1 is added to yz
- The characters are moved to the Alpha register: CHR(wx+100) & CHR(yz + 1)
- Decryption to get f[..] is the reverse process: f[..] = VAL(wx) – 100 + VAL (yz) – 1
The initialisation of f[..] with value 2000 is a sequential process thereby creating records and appending characters as per definition of the number of records and bytes per records from the lookup vector.
For retrieving and updating the value of f[..] the pointer depends on the value of b. This calculation is done from line 89 onwards and is based on the algorithm. Please note that the integer part points to the record and the decimals (division by 1000) point to the first character of the two-byte value of f[..]:
Several tests have been conducted to verify this pointer calculation process with sample values:
Because the GETREC instruction moves the pointer to the end of the copied part record the pointer must be set twice, for decryption and encryption (after updating f[..]). The pointer is calculated once and stored in R09. In the link to the program package (below) the program listing is also provided with comments.
Runtime
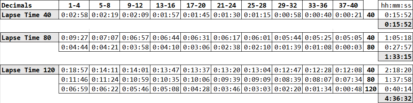
Running the program Is more of a nostalgic interest because the performance is extremely low due to the number of loops (see first table) that needs to be handled. Simulations using the HP-41CX emulator V41 on maximum speed and turbo show that the runtime varies from 15 minutes, 1.5 hours to 4.5 hours for determining 40, 80 respectively 120 decimals:
Compared to the HP-41CX’s performance, these runtimes could easily be multiplied by a factor 4.
Example
Program Listing
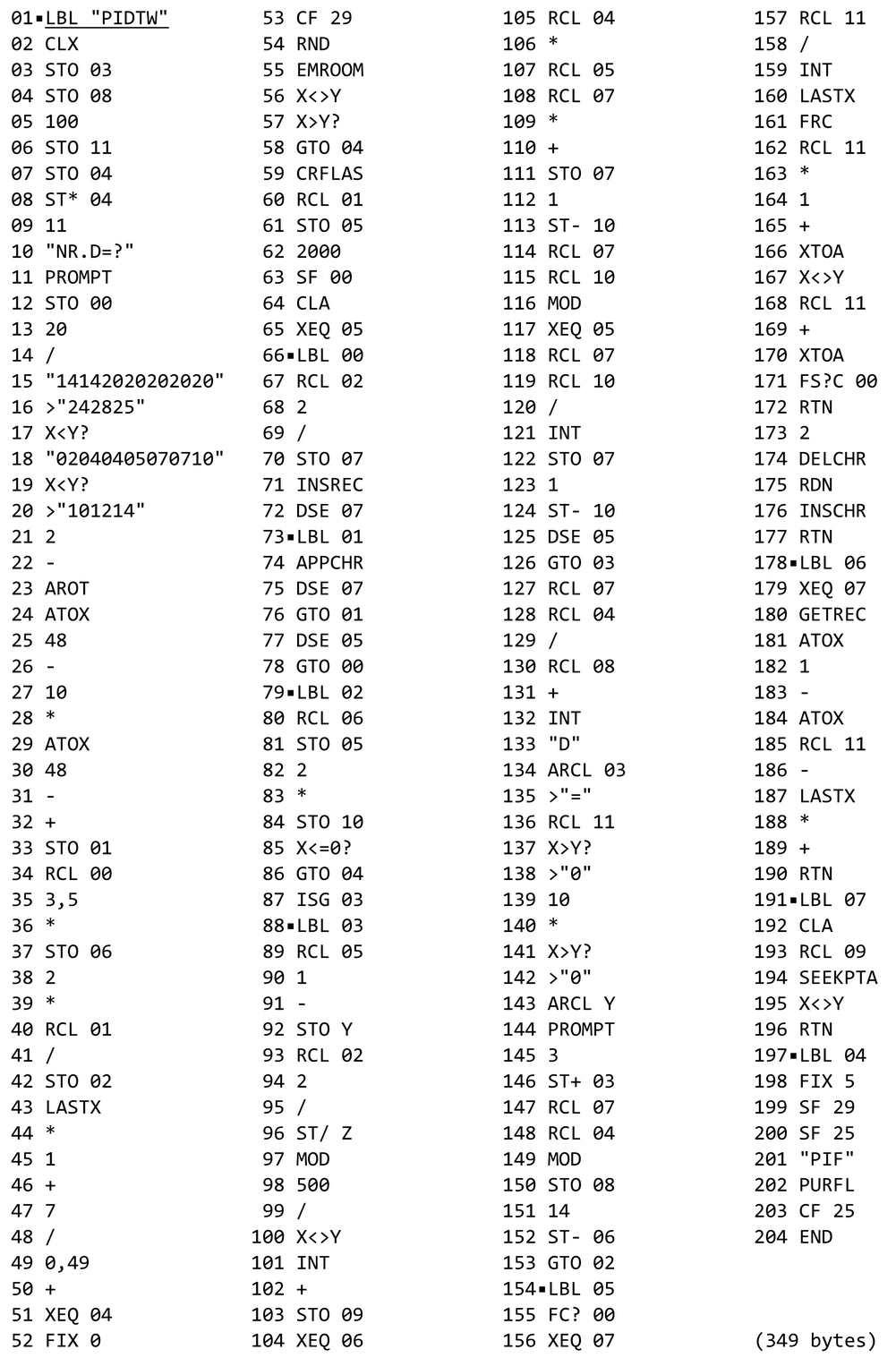
The listing of PIDTW is given below.
Registers, Labels and Flags
Downloads
PDF format of program PIDTW.
RAW/TXT format of program PIDTW (in zip file).
© 2006-2022 by Auke Hoekstra
